歴史のなかでは1+1=2が実際に成立したことは一度もない
2019年10月12日
*この記事は筆者が日本語と韓国語の2カ国語で執筆しました。韓国語版(한국어판)でもご覧ください。
一人のみなしごの少年がいた。親の顔も知らないまま施設を転々としながら育った。彼にとっていちばん羨ましいことは家族があることだった。親や兄弟がある友人をみると、胸が空洞になったように妬ましく、孤独だった。
しかしそんな困難な境遇にもかかわらず、彼はまじめに勉強し、熱心に仕事をしていつのまにか立派な社会人になった。そして自分とよく似た境遇の少女と出会った。
彼女もやはり孤児として困難のなかで育ってきた。二人はすぐに心が通じた。二人はそれぞれにいつかだれかと結婚し、大家族のなかで、経済的にも裕福に、楽しく賑やかに暮らすことを願っていたが、彼らの境遇ではそのような相手と出会い結ばれることはかんたんではなかった。彼らがみなしごであることは、常に彼らにつきまとうマイナス条件だった。
青年はある日決心して彼女に手紙を書いた。
できるならば私はあなたの夫になりたいです。そしてあなたがずっとほしかったあなたの父にもなります。それだけでなくオマケとして、あなたがひとりいればなぁと思っていたお兄さんにもなります。そしてもちろんこれからあなたが生んでくれる息子と娘のお父さんもなります。
この手紙を受けとった孤立の少女は胸があつくなった。今まで夢みてきた家族がそのなかにぜんぶ入っていたからである。だからじっくり考えてから返信を書いた。
それなら私もあなたのために何でもいたします。もちろんあなたの一番の妻になります。そしてあなたがずっとほしかったあなたのお母さんにもなります。それだけでなくオマケとして、あなたがひとりいればなぁと思っていた妹さんにもなります。そしてもちろんあなたの息子、娘の良いお母さんになるようにいたします。
これは実話である。
少年の孤独1と少女の孤独1、これを合わせると、普通1+1=2の計算式が成り立ち、答えは孤独2となるはずだ。一般に、天涯孤独の二人が結婚をすると、さらに孤独が深まり、生きづらいともいわれるところである。
しかしさきの二人は違った。孤独1に他の孤独1を足し算したにもかかわらず、計算をしてみると夫1、妻1、父1、母1、兄1、妹1、息子、娘それぞれ2人ずつ産んだから、あわせて子ども4人、最終的には家族が10人いるようなことになった。
だからここでの計算式は「1+1=10」となるのだが、さてだれがこれを間違っているといえようか。
もちろん1+1の答えはたいていの場合2になる。しかし、私たちが自らの生活と夢のなかに見出そうとする人間らしい価値においては、柔軟に考えれば別解の可能性はいくらでもある。

 筆者は建築を好む。美しい建築は人を気持ち良くさせる。筆者が好むのは、華やかで高級な建築ではなく、しっかりと人を愛する建築である。ほとんどの真の建築家は科学者であり、人文学者であり、芸術家であると思う。写真は筆者が好きな日本の現役建築家の安藤忠雄の作品姫路文学館(1992年)=姫路文学館HPより
筆者は建築を好む。美しい建築は人を気持ち良くさせる。筆者が好むのは、華やかで高級な建築ではなく、しっかりと人を愛する建築である。ほとんどの真の建築家は科学者であり、人文学者であり、芸術家であると思う。写真は筆者が好きな日本の現役建築家の安藤忠雄の作品姫路文学館(1992年)=姫路文学館HPより日本のテレビ番組(テレビ朝日)、「劇的ビフォーアフター」(before and afterの意)をご存じだろうか。古い家を深いヒューマニズムの持ち主であるリモデリング専門の建築家たちがまったく新しい空間に再創造していくプロセスを放送する番組である。
建築にかかわる番組であるから、所与のスペース、建物の駆体構造などの条件に従って厳密な計算が求められることはいうまでもない。しかしこのプログラムの白眉は、その家で幸せに暮らしてきた家族一人一人を深く配慮する建築家の心遣いを映し出すことにある。
年老いた両親がいる場合には、その健康状態、長年の趣味、そしてもっとも重要なこととしてその人が守ってきた価値観や具体的な事物などを、新しい家の空間設計に際して勘案する。
もし障害者が家族にいる場合には、その人に最大限の自由を保障できるように家のスペースと設備を計画する。そして子供たちは子供たちなりに、学生は学生なりに、主婦は主婦なりに、それぞれの役割と行動範囲、そしてなによりもそれぞれの幸せという条件が、スペース効率を圧倒しつつ建築計画に反映される。
ここには「数学的計算」と「人文学的計算」のみごとな調和がある。
そこではただ便利で、丈夫で、新らしいだけの家ではなく、家族をひとつにするための空間が再生されるのだ。そして再生されたスペースを目の前にして、多くの家族が涙を流し、感動的な幸せを経験する。そこにはあきらかに人文学的計算式が成り立っているといえよう。
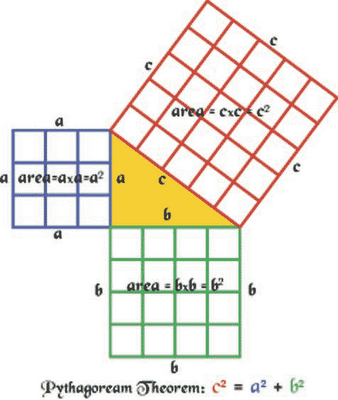 「ピタゴラスの定理」= 筆者の講義資料より
「ピタゴラスの定理」= 筆者の講義資料より歴史学の方法論を駆使する筆者の宗教講義では、まず歴史自体に対する説明をおこなう。歴史をどのように理解するかという説明には、数学の話も登場する。「ピタゴラスの定理(Pythagorean theorem)」である。
ここに完璧な直角三角形があるとしましょう。直角辺の二乗にもうひとつの直角辺の二乗を加えた値は斜辺の二乗の値と一致します。この 「ピタゴラスの定理」は、永遠の数学的真理であることが明らかですが、しかし歴史上の実際には一度も実現したことがありません。なぜなら私たちは完璧な直角三角形を描いたり作成したりすることができないからです…
通常ここまで説明すると、クラスは沈黙のうちに「え、そう? 本当にそう? じょうずに作図すればできるんじゃない」と言いたげな雰囲気になる。そして学生のなかには、コンピュータを使って正確に描画しようとする学生が…だが彼は途中で気づいて停止する。
その後筆者は、私たち頭の中では完璧な直角三角形をいくらでも書くことができると伝える。想像と仮定、理想的な概念としては可能であるという。それだけでなく、近似としてならば限りなく完璧な直角三角形を書くことができるだろうと補足する。
しかし完璧な直角三角形、それ自体は実在しない。
再び1+1=2にもどる。
果たして1とは何なのか。私たちが「ひとつ」というとき、それがどのような構成、単位、範囲、主体によって決定されているのかによって「ひとつ」は複数にもなるので、歴史のなかでは1+1=2が実際に成立したことは一度もない。ただ概念として「ひとつ」に「ひとつ」を加えると「ふたつ」になると考えているだけだ。
筆者のクラスはだいたいそれを受け入れる。だから歴史は数学と最も遠いところで、そして歴史は私たちのすぐ近くに、そのようになにかが欠けたまま、不完全なままあると説明する。するとある学生は、ひとりごどのようにつぶやく。「だから僕は数学ができないんだ…」。なんともかわいらしい反応ではないか。
歴史は私たちの存在自体であるか、そうでなくても私たちの非常に近くにあるが、その歴史的実在ともっとも遠いところにある別の真理が数学なのだと説明すると、すぐにそんなに遠くにあるものだから自分は数学を苦手なのだという。数学嫌いの彼は、そんな「メタファー」(metaphor)をよく応用して人文学の勉強を頑張るはずであろう。筆者もにんまり笑ってあげる。本当にそのとおりだと。
筆者は強力な反戦主義者である。どんな理由や名目があっでも戦争は許せない。たとえ「防衛戦争」という概念をもちだされても、それさえも避ければ避けられるものだろうと信じている。
戦争は人類が犯した罪の中でもっとも重い罪悪である。遠く離れた事例をいうまでもない、身近なこととして日本と韓国の歴史を振り返るだけでも、戦争はもっとも残酷な状況とトラウマを作り出したことをすぐに確認できる。
とりわけ、戦争では相互彼我共にその社会のいちばん弱い人々が甚大な被害をこうむる。むしろ戦争を主導してそれを実行する人々より、それに反対する一般の人々のほうがすさまじい状況下におかれる。戦争は多数の民衆の「血の川」を生み出す。
人文学的思考は、戦争を避けるための思考にもっとも近接している。どんな地域や国でも戦争が過ぎ去った後の時空間には、歴史的にみてものすごく大量の人文学的な省察がおこなわれる。文学が書かれ、歴史が記録され、数多くの物語が紡がれる。
戦争は許せないということだけが、人文学の省察の到達点であり歴史である。真の人文学的計算は、数の多少を問わず人々が犠牲になってはじめて到達するそのような地点について、結局は答えはマイナスであると主張する。
 1950年の朝鮮戦争の惨状=大韓民国歴史博物館HPより
1950年の朝鮮戦争の惨状=大韓民国歴史博物館HPより最近のニュースに次のような言説があった。朝鮮半島で戦争が起きた場合、最小限に見積もって約100万人の犠牲を覚悟するなら韓国の統一は可能であるという。これこそまさに反人文学的な思考である。
筆者は、統一がたとえ韓国人の「夢にも想う願い」であり、もっとも貴重な「価値」であるとしても、100万人の命を代価とすることは愚かであり、沙汰の限りであると思う。7000万人が幸せになるために100万人の犠牲を是とするという考え自体が論外であり、反人文学的思考である。
戦争に勝つことより戦争を防ぐことがだいじである。戦争のあとでその惨状を省察し、それは絶対に悪であるとすることも人文学のつとめだが、それよりもまず戦争を防ぐことの大切さを、そのような考え方の尊さを主張し続けなければならない。プライドを守るために戦争に勝つのではなく、プライドを捨てても戦争を止めなければならない。指導者のプライドや政治家の威信、軍人の名誉より大切なものが民衆多数の生命であり、民衆の命こそがもっとも高貴な存在であることを世に知らしめるのが人文学の仕事である。
戦争近しのニュースが、戦争の兆候が荒々しく伝えられるなか、人文学者はこう考える。戦争に勝つ方法を考える者は、一日も早く戦争を止める方策をみつけることに没頭しなければならない。報復を考えている者は報復する必要がない条件を作るしかない。相手にそれができない場合には、私たち自身がそうしなければならない。
筆者は、ときに障害者として特別扱いを受けるときがある。「例外」(exception)としてなにかをすることが認められるのであるが、実のところ例外的な取り扱いをされることはそんなに気持ちの良いことではない。
しかしそんなときもこれは「例外」扱いではなくて、そのような「待遇」を受けているのだと考えるようにしている。例外と待遇の関係は紙一枚ほどの違いである。例外的な存在、少数者、「マイノリティ」(minority)がどのような取り扱いを受けているかによって、ひとつの国、社会、コミュニティのレベルが測られる。
筆者は幼い時代から社会生活をはじめた後にも、つねに歯をくいしばって例外的存在ではないことを目指して生きてきた。気を集中して、努力を重ね、少なくとも全体の隊伍から離脱しないことを目標としてきた。そうではないと、特に韓国社会では、不利な条件下にある人間が自分の最低限の権利を守って生きることさえ不可能だったのだ。
いまでは筆者もすこし変化したが、誰かにちょっとした助力を受けるときにも、それが憐れみではないかと疑うことがあり、できれば自分自身の力で克服しようとする意志がなによりも重要な価値であると思って生きてきた。
障害を持つ人間が社会の中でそれなりの役割を果たしたり、目標を達成したりすると、「隊伍離脱不可原則」とでもいうべきものによって脚光を浴びることがある。筆者もやはり例外ではなくその原則に身を寄せて「人間劇場」を自己演出して生きてきたのかもしれない。
もちろんそれには非常に良い面もある。不利な条件を背負っている人間がより堅剛に、よりたくましい独立心をもって、感動的な勇気をみせることもあろう。
徴兵制の韓国で、筆者は軍隊にいかなかった。しかし筆者は誰よりも軍隊での話をよく知っている。若い時代に比較的長い軍隊生活を経験した筆者の友人たちは、いつも筆者に軍隊生活の話をしてくれた。友達だけでなく、後には筆者の教え子たちも軍隊経験がある場合には例外なくそうした。
そこには「非常に良いわけ」とちょっと「けしからんわけ」のふたつがある。
良いわけとは、軍隊を知らない筆者に配慮して詳細にその体験を伝えることで、筆者に間接的にでも知識を与えようという意図である。
しかし一方ではつぎのような事情も考えられる。軍隊経験がある人たちはたいがい自分の経験を誇張して語りたがる。いわゆる「愛嬌ある詐欺」であるが、ただそれを軍隊経験者にいえば、すぐに誇張がばれる。その点、経験がない筆者にはある程度の「嘘」が通じる。
これはおそらく、韓国の数多くの女性たちが男性の果てしなく続く軍隊話を聞くことを余儀なくされていることと一脈通じている。特に軍隊でのサッカーや足球(ジョック)の話を聞かされることは、女性たちにとってもっともつまらないことの定番である。
ところでそんな話のなかで筆者がもっとも興味深いのは、通常どの部隊にでもいる「顧問官」(軍営での俗語として「のろま」「間抜け」の意味) すなわち「例外者」のことである。
いま思えば、軍隊という統一された団体組織のなかでもっとも「人文学的存在」が彼ら「顧問官」と揶揄される「例外の存在」ではないかと思う。彼らの存在がなければ軍隊はどんなに索漠とした組織になることか。
こんなことをいえば、筆者の友人たちは、やはり君は軍隊の経験がないのですごくロマンチックに考えてるねと指摘するかもしれない。平時の軍隊では「顧問官」の存在はときに面白おかしく語られ、知られるところであるが、戦時下や激しい訓練のなかでは、彼らのために全隊が絶体絶命の危機に直面することになるかもしれない。それはやはりたしかなことだ。
いずれにせよ人文学は、統一的な思考や組織、条件、一律的な成果や正解からはほど遠い。ユニークでとんでもなくて、非常に例外的な「顧問官」といった「例外の存在」が人文学的価値とよく通じるという筆者の考えは堅固である。 (続く)
 DanieleGay/Shutterstock.com
DanieleGay/Shutterstock.com有料会員の方はログインページに進み、デジタル版のIDとパスワードでログインしてください
一部の記事は有料会員以外の方もログインせずに全文を閲覧できます。
ご利用方法はアーカイブトップでご確認ください
朝日新聞社の言論サイトRe:Ron(リロン)もご覧ください