2011年11月12日
==============================================
朝日グループのジャーナリズムTV「朝日ニュースター」は、通信衛星などを利用して24時間放送しているテレビチャンネルで、ケーブルテレビ局やスカパー!などを通じて有料視聴することができます。4月から始まった新番組「科学朝日」は、高橋真理子・朝日新聞編集委員がレギュラー出演する科学トーク番組です。WEBRONZAでは、番組内容をスペシャル記事としてテキスト化してお届けします。
====================================================================
ゲスト 東北大学多元物質科学研究所教授 蔡安邦さん

高橋:こんばんは。科学の最先端にひたる「科学朝日」。案内役の高橋真理子です。本日取り上げるテーマは、「第3の固体、準結晶とは何か」です。今年のノーベル化学賞は、イスラエル工科大特別教授のダニエル・シェヒトマン氏に授与されることが決まりました。理由は、「準結晶の発見」です。準結晶とは、いったいどんなものなのでしょうか。その発見には、どんな意味があるのでしょうか。本日は、準結晶の秘密に迫ります。ゲストはこの方。世界の準結晶研究をリードしてきた、東北大学多元物質科学研究所教授の蔡安邦さんです。蔡さん、よろしくお願い致します。
蔡:こんばんは。よろしくお願いします。
高橋:本日のテーマである「準結晶」ですが、視聴者の方には初めて聞いたという方も多いかもしれません。物質には、気体、液体、固体の3つの状態があることは、学校の理科の授業で習うんですけれども、気体というのは、原子が自由に動き回っている状態。液体は、ある程度自由に動き回っている状態。固体は、原子同士が手をつないで動けない状態にあると。その固体の中で規則正しく手をつないでいるものが、結晶と呼ばれ、不規則にがちゃがちゃの状態でいるのが、アモルファスと呼ばれるものですね。アモルファスというのは、要するに、ガラスがその代表例とされている。そうすると、準結晶というのは、結晶に準じるという字を書くわけですから、結晶と似てるけどちょっと違うと。そういう意味なんでしょうか。
蔡:最初は、そう思われていましたが、実は、今になって準結晶は、結晶に準ずる構造っていうよりも、全く結晶と異なる新しい物質構造だとわかってきた。ですから、全く新しい、違う秩序を持っている構造です。
高橋:ただ、シェヒトマンさんが、最初に見つけられた時は、それは本当かどうかってずいぶん疑いの目で見られたそうですね。
蔡:そうですね。というのは、最初、発見された準結晶は、準安定で不安定で、ちょっと温度を上げると結晶に変わってしまう。もう1つ理由は、金属液体の急速凝固でつくられたものなので、非常に乱れているんです、構造的に。
高橋:金属を液体の状態にして、それを素早く冷やす。
蔡:そうですね。そのために非常に構造が乱れているわけです。
高橋:急速に冷やすと、構造が乱れるんですか?
蔡:そうですね。でも、全体的に準結晶のような構造が見えたわけです。でも、やっぱりいろいろ議論をする余地があったんです。
高橋:どうも怪しいと。ノーベル委員会が発表したプレスリリースに、非常に面白いエピソードが書いてあったんですけれども、そのシェヒトマンさんが、不思議なものを発見したということを所内の同じ研究者に言っても、なかなか信用してもらえなかった。所長さんは、結晶学の教科書を持ってきて、これを読めって言ったそうですね。
蔡:そうですね。それは、従来の結晶では考えられないことなので、あなた、もうちょっと勉強しなさいって教科書を渡されてというエピソードを私も聞いたことがあります。
高橋:それぐらい信じられていなかったんですけれども、学界の方々が信じるようになった、そのきっかけをつくったのが、蔡先生がおつくりになった結晶だったというふうに聞いてますが。
蔡:それは、1つのきっかけです。先ほど言ったように、準安定ということは、構造が乱れるということで、何も新しい準結晶っていう概念で考えなくても説明ができました。例えば、結晶と欠陥の共存、あるいは混ざっている状態、あるいは、結晶とアモルファスの中間状態というような、今までの物質構造の範疇で理解、あるいは説明できてしまうんです。そういう意味で、これは単なる出来損ないの結晶なのかというふうに見ている人もいました。
ですから、いろんな反対があったわけです。従って、私が、学生の時から、1987年に初めて安定な準結晶を1つだけじゃなくて、いろんな合金で安定な準結晶を作成して、それが、結晶と同じようなレベルの高い秩序、あるいは品質を持っていて、いろんな物質の普遍性が確認されたわけです。その関係で、広く受け入れられるようになったっていうような、そういういきさつがあると思います。
高橋:そうなんですね。それでは、CMを挟んで、準結晶について、さらに詳しく伺います。いったんCMです。
~CM~
高橋:「科学朝日」本日のゲストはこの方、東北大学多元物質科学研究所教授の蔡安邦さんです。改めましてよろしくお願い致します。
蔡:よろしくお願いします。
高橋:本日のテーマは、「第3の固体、準結晶とは何か」です。あらためて準結晶とは何なのか、分かりやすく説明していただきたいと思います。
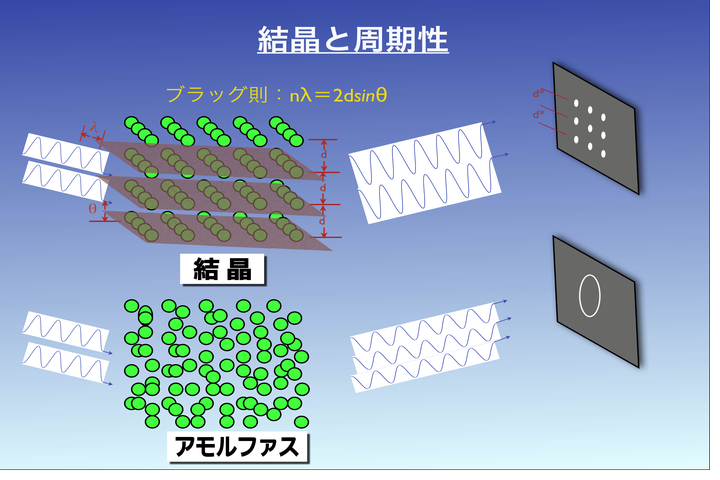
蔡:準結晶を説明する前に、まずは、結晶とは何かを説明しないといけないですけれども、こちらの図を使って説明させていただきます。準結晶が発見される前には、物質を構造で分類すると、アモルファスと結晶と二通りがありました。さっき説明されたように、ばらばらと、秩序がないと。結晶は、こういうふうにきちんと原子が、並んでるような構造でして、根本的な違いというのは、結晶では、きちんと並んで原子面が見えます。
高橋:原子面というのは、その平面のことですね。並んでいる面。
蔡:そうですね。原子が、きちんとある面に沿って並んでいます。この原子面が存在するために、われわれは、エックス線、あるいは電子線を使って、その構造を調べることが可能です。そこで重要なのは、いわゆる回折現象です。
高橋:回るという字に折ると書く回折。
蔡:それは、例えば、エックス線とか、あるいは電子線というのが、波として入ってきまして、ここの面に対して同じように回折される、透過する分もありますけども。結晶というのは、原子面がある故に回折を起こして、ここである条件、いわゆる波長とか、面間隔がある条件を満たしたときに、この原子面とこの原子面から回折された波が強めあって、回折点をつくるわけです。
高橋:山と山、谷と谷がそろって、エックス線が届くところは、そっちの明るい場所になるわけですね。ちょうど反対同士が組み合わさると、暗くなるんですよね。黒いところに明るい点々ができてくると。それは、結晶の場合である。
蔡:そうです。そのとおりで、そこは非常に重要な1つの条件があって、例えば、原子面の間隔は、等間隔でないといけないです。いわゆる周期ということなんです。この周期があって初めてこの条件を満たして、これが、回折点をつくるわけです。
高橋:なるほど、なるほど。
蔡:逆に言うと、つくった回折点も必ず周期的に等間隔で並ばないといけないんです。こういうふうに回折点が理解されてきた。
高橋:ばらばらのアモルファスの場合は、通ったエックス線は、そっちもばらばらになるから。
蔡:相関がないですよね。相関がないというか、はっきりした原子面がないから、どこからでも散乱されるんです。ただ、ある程度、原子と原子の距離を平均とったところで、なんとかぼやっとリングをつくるようなことになるんです。
高橋:そういう映像が撮れるんですね。でも、アモルファスか、斑点が出てくる結晶か、固体にはその2つしかないと思われていたわけですね。
蔡:そうです。そこで大事なのは、結晶というのは、後で出てきますが、周期性です。回折反射も必ず周期性を持たないといけないと古くからそういうふうに理解されてきました。
高橋:そうやって撮った写真の例ですね。
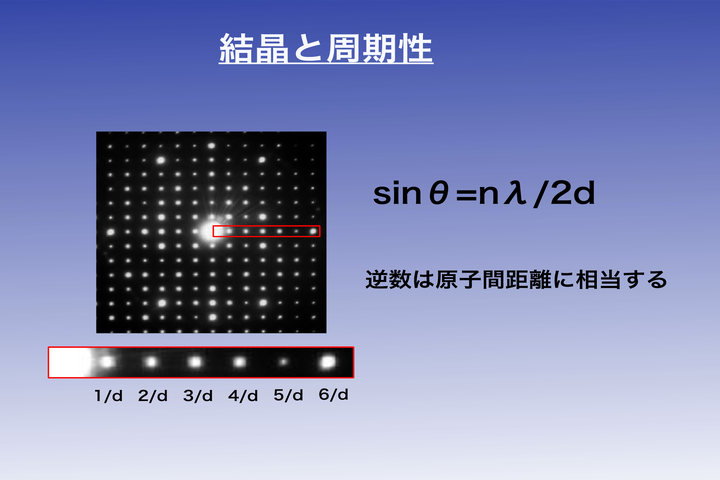
蔡:一例をお見せしますと、これは、電子顕微鏡で撮った回折像なんです。中心から見て、反射を拡大してみますと、見ていただくと分かるかと思いますが、全部等間隔になっているんです。
高橋:そうですね。
蔡:それは、さっきの式を書き換えると、nという数字は整数なので、それが存在する故に周期性というのは必ず存在するわけです。
高橋:1倍、2倍、3倍、4倍、5倍の距離で並んでいるということですね。
蔡:これは、ちょっと難しい言葉なんですけれども、逆数でとっているんです。原子の位置も逆数。ですから、その距離というのは、回折点があって現れてるものというのは、逆空間点とわれわれは呼んでいるわけです。いわゆる逆です。われわれ人間の生きた空間ではなくて。
高橋:ここの写真に撮られている空間というのは、逆の空間である。
蔡:逆の空間ですよね。
高橋:光の点は、ちょっと明るいのと、それほどでもないのとありますよね。それは、何を示してるんですか。
蔡:これは、先ほどのエックス線の回折原子面が多ければ多いほど、その強度が強くなる。
高橋:多いと強度が強い。
蔡:そうです。それがあって、例えば、構造を解析するのに、この回折点の位置とあるいはこの強度。その情報を全部ひっくるめて、どこにどういう原子があるのか。今まで結晶でそういうふうに決めてきたわけです。
高橋:これだと5番目のが、ちょっと小さいですよね。
蔡:例えば、原子面の数が少ないとか、存在すれば、それが弱く出るんです。
高橋:すると、この逆空間の写真から原子がどう並んでるかっていうのが、分かっていくと。
蔡:ある程度は分かるんです。
高橋:それが、結晶研究の普通の研究方法であったわけですね。
蔡:そうですね。とにかく重要なのは、繰り返してきましたけども、周期性っていう言葉です。いわゆる実空間での原子の並びも周期性もっているし、逆空間の回折点にも周期性があるっていう、そういう相関が必ず成立するわけです。それがあっての結晶と今までいわれてきたんです。
高橋:周期性とは、要するに同じ間隔で並んでるってことですよね。
蔡:そう。等間隔ということです。
高橋:次のスライドは。これはなんでしょうか。
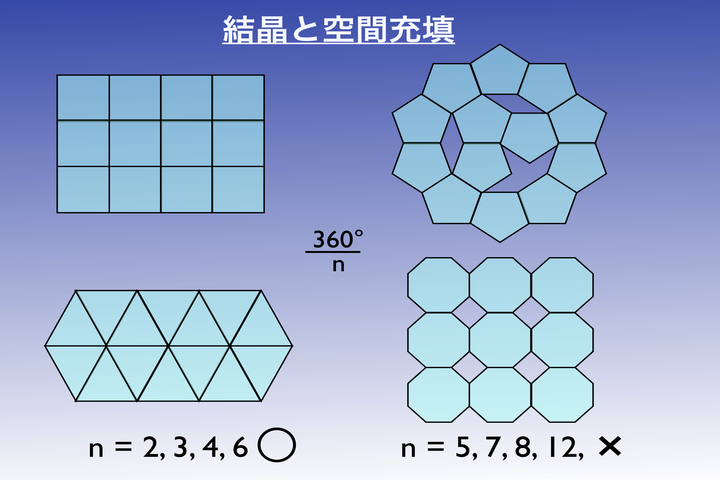
蔡:実空間でいうと、結晶というのは、ある図形を使って、平面、あるいは空間を埋め尽くしていくわけです。その場合は、それができるものとできないものがありまして、できるものというのは、ここで示すように正方形、あるいは正三角形、あるいは正六角形となります。ところが、五角形を使うと、あるいは八角形とかを使うと、こういうすき間が出てきます。
高橋:埋め尽くすことができないですね。間にすき間ができてしまう。
蔡:そうですね。
高橋:このnっていうのは、360度を幾つで割るかっていうnですね。2で割ると180度で、これはただの直線ですけども、3で割ると120度。
蔡:六角形、三角形です。
高橋:六角形では埋め尽くせると。4で割ると90度だから四角ですね。四角は大丈夫ですと。6で割ると60度で正三角形で、これも埋め尽くせますと。今度、5で割るということは、五角形ができるわけですね。それは、埋め尽くせないし、7も絶対駄目そうですね、見るからに。
蔡:そうです。7も駄目です。
高橋:8は、いけそうですけど、駄目なんですね。
蔡:8も駄目なんですよ。
高橋:12も駄目なんですね。
蔡:そうですね。
高橋:すると、たったこの4種類しかないんですか。
蔡:1もあるんですけどね。だから、5種類です。1は、何も対称性がないものなんですよね。
高橋:そうですね。
蔡:ですから、形というのは5種類で、1、2、3、4、6の対称性です。
高橋:1も足せばね。結晶がそうなっているっていうことは、さっき言った逆空間、エックス線で撮った写真も、その5種類の対称性を持ったものしかないということだったんですね。
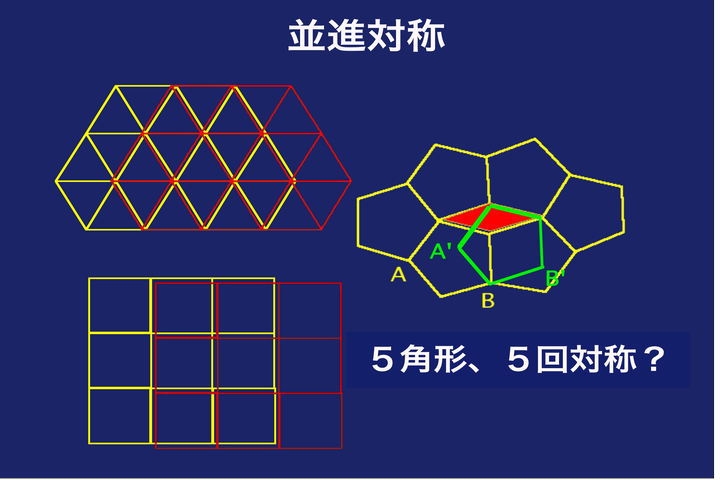
蔡:それに対応するわけです。もう1つ、次のスライドを。別の見方をしますと、例えば、基本的に結晶というのは、一つの単位を使って、それを繰り返せばいいわけです。それを繰り返した結果、例えば、こういう図形になりますと、例えば、ここからちょっと分かりにくいですか。例えば、1単位の距離を平行移動させても、全く同じ、元と同じ、変わらないという図形がつくれるんです。それは、今言った三角形、六角形、あるいは四角形でも、あるいは正方形でも、全部できるんです。これは、いわゆる並進性です。この並進性を満たす対称っていうのは、さっきと同じように3回、4回、2回、1回とか、6回。ところが、5回の場合は、ここで見ていただくと分かるように、五角形をここに移動させると、ここは何も無い、新しいものができてしまうんです。そこは、今までの結晶の定義からすると、具合が悪いんです。だから、五角形、あるいは5回対称のものが、許されない。
高橋:結晶には、そういうのはない。並進とは、要するに横にずらすと。横にずらしたときに、元と同じ形にぴったり重ね合わすことができる。そうじゃないと結晶はできない。それはそうですよね。結晶だって、空間の中にそれが埋まってるわけですから。五角形じゃすき間ができちゃって駄目ですよね。
蔡:そうですね。やっぱりそこは、一つの単位で全部考えてつくってしまうという結晶の概念ではあり得ないですね。
高橋:そうですね。あり得ないですね。実際、自然界に見つかっている結晶というのも、大体六角形とか、四角形ですね。
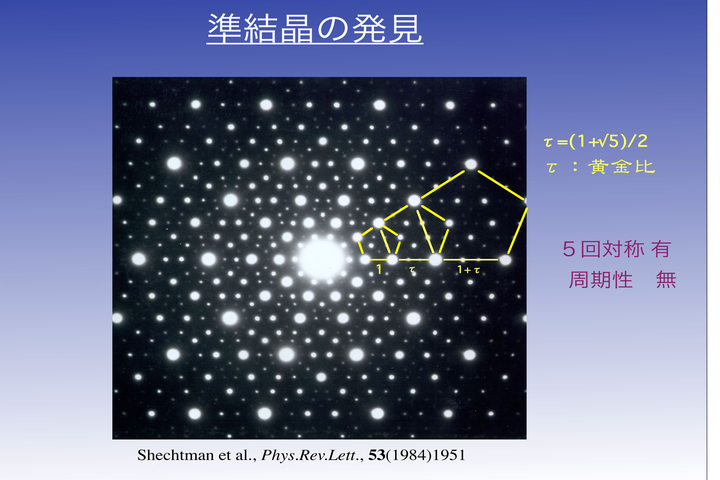
蔡:そうですね。例えば、水晶だとか、食塩だとか、そういう単位のもので積み上げてできたものなんですよね。ところが、それに対して準結晶というのは、さっきの定義をもう一度思いだしていただきたいんですけども。まず、さっき言ったように、結晶というのは周期性がある故に、回折点がつくれるわけです。つくった回折点も等間隔、あるいは周期性を持たないといけない。ところが、この回折点の配置を見ていきますと、等間隔ではないです。
高橋:そうですね。だんだん長くなっていますね。
蔡:実は、この長さですが、中心からとっていくと、ある規則になっているわけです。黄金比になっています。これは、後でまた説明いたしますけども、黄金比になっているわけです。これは、すでに結晶の概念というか、結晶の定義にやっぱり反してるわけです。スポットが、反射が、回折点が出ているのに、等間隔ではない。
高橋:そうか。アモルファスだったらば、スポットは出ない。ほわほわほわとしているのしか見えない。スポットがきれいに見えているんだけれども、等間隔ではない。そこで結晶ではない。確かに不思議な存在ですね。
蔡:もう1つは、見ていきますと、五角形、実際は十角形にもありますけど、ここで五角形を取り上げて説明しますと、さっき言ったように、1個1個の回折点というのは、一つ一つの原子面に対応するわけです。五角形をつくるということは、そういう原子配置が、五角形の配置をつくっているっていうことを意味してるわけです。ですから、ここから分かることは、回折点が出ているのに周期性が等間隔ではない。しかも、結晶が今まで許されない5回対称が存在しているという2つです。そこでやっぱり発見された当時は、かなりいろんな衝撃を学界に与えたわけです。
高橋:結晶とは何か、それから回折写真とは何かということが、分かってからこの写真を見ると、すごく不思議だというのが分かりますが、そうじゃなくてただ見ると、単にきれいに規則的に点が並んでるように見えてしまうんですけれども。
蔡:そのとおりです。私も学生のときからこの仕事を始めたんですけども、最初見た感じで、美しさに取り付かれたんです。
高橋:そうですよね。
蔡:五角形はやっぱり不思議なものがありますね。
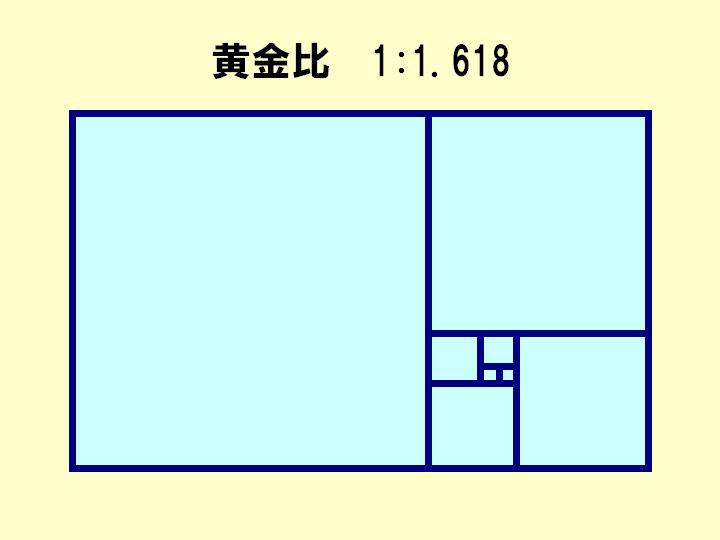
高橋:それで、今出てきた黄金比という言葉ですけど、数学でよく聞くんですけれども、長方形の中で一番美しく見える長方形の縦と横の比。これが、黄金比だというふうによく説明されます。そういう理解で間違いないんでしょうか。
蔡:それは間違いないですけれど、ここに書いている図というのは、黄金長方形というものでして、辺の長さの比が黄金比になってるんです。
高橋:1:1.618。これはずっと続くんですよね。
蔡:一つの正方形をとって、残りのこっちのほうが、またそれになるわけです。ずっと切っていくと、全部黄金の比をとっていくと、どんどん、いろいろ小さくつくれるわけです。
高橋:正方形を切り取った残りの長方形も、黄金比になっているんですね。黄金比って、名刺の大きさなんですってね。私が使う名刺は、黄金比になっているそうです。やっぱり人間が、快適と感じる大きさだそうですけども。でも、快適と感じるだけじゃなくて、正方形をとったら、また残りの長方形が、黄金比になっているっていう不思議な性質を持っているわけですね。
蔡:そうなんですよね。非常に神秘な数字ですね。
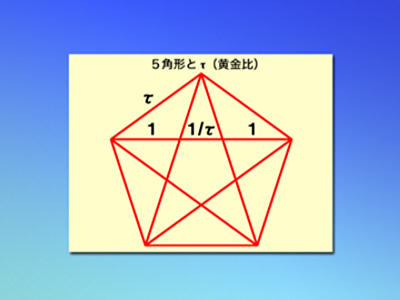
高橋:五角形にもこの黄金比が出てくるんですよね。
蔡:そうです。実は、五角形というのは、5個の辺と一対の対角線との比が全部黄金比になっているんです。
高橋:どれとどれが、1対…。
蔡:例えば、タウ対角線と辺の比が。
高橋:タウっていうのは、さっきの1.618ですね。この対角線を1だとすると、辺が1.61…。逆ですね。
蔡:逆です。こっちが1.618とすると、こっちが1です。ですから、ちょっと不思議な数字なんですけども。逆にここが1となると、こっちがタウ分の1なんです。
高橋:タウ分の1。逆数ですね。
蔡:そう。1.618ですよね。1.618の2乗は、2.618です。1.618分の1は、0.618です。だから、その比も同じようなタウになっているわけです。さらに、この中の対角線を切って分割していくと、こっちの長さとこちらの長さも、また黄金比になっているんです。さらにこちらを切っていくと、今度こちらの長さとこちらの長さも、また黄金比になってるわけです。だから、どんどん一回りずつ小さくなっていっても、黄金比の関係が保たれているわけです。
高橋:星形がきれいに見えるというのも、それと関係しているんですか。
蔡:そうかもしれないですね。五角形というのは、なんとなく不思議な魅力を持っているわけです。
高橋:じゃあ、結晶のさっきの写真に黄金比が出てきたということは、まさに結晶構造の中に五角形が入っているということを示していることになるんですね。
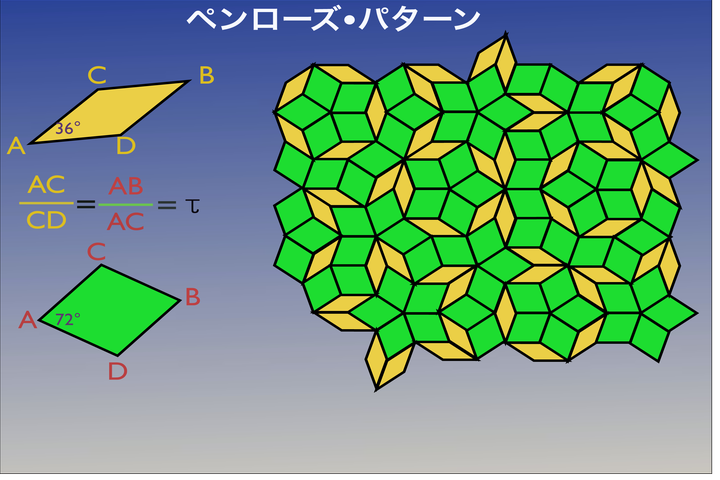
蔡:そうです。しかし、今、結晶では説明できない回折像が出てきたわけです。実は、準結晶が発見される前に、ペンローズという数学者が、非周期的に平面をすき間なく埋め尽くす方法を考案したんです。こういう図形を考案したわけです。この図形にもやっぱり黄金比が存在しているわけです。彼が使った二つの四角形、あるいはひし形が、このような角度になっていて、いずれもこちらの辺と短い対角線との比がタウになっている。あるいは、この太ったひし形ですと、対角線と辺の比が、タウになっているわけです。この2種類のひし形を使って、一定の法則に沿って、無秩序じゃないですよ、ちゃんとした法則に従って、敷き詰めていくと、このようなパターンがつくれるわけです。
高橋:敷き詰められることができると。それで、五角形とか、十角形みたいな一つの固まりが見えますよね。
蔡:十角形もありますね。これは、五角形もあります。
高橋:十角形があるけど、ちょっと外れたとこの十角形は、構成要素が全然違ってますよね。
蔡:そうです。
高橋:緑が5つあって、周りに黄色っていうんで十角形もできているし、もっと変な形で、黄色がこう、途中、途中、変なかたちで入ったような形での十角形もありますね。
蔡:そうです。
高橋:確かに横にずらして、重なるかっていうと、全然重ならない感じですね。だけど、規則はある。
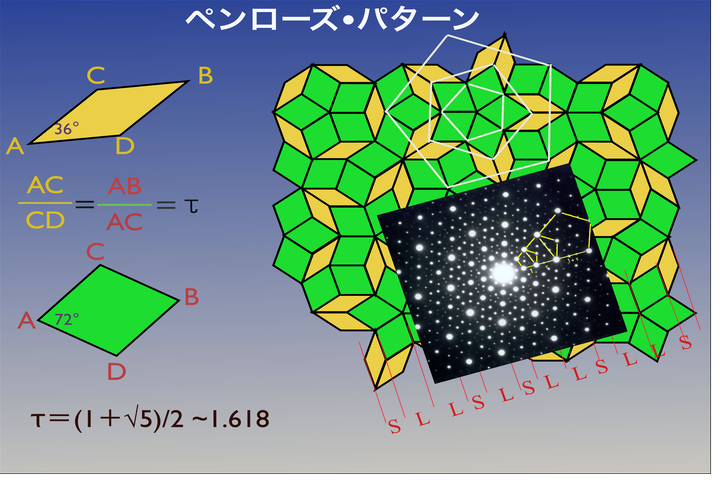
蔡:規則はあるんです。一定の法則に沿ってやるわけです。実は、これが準結晶の構造の元になってるわけです。例えば、こちらの図形を光反射を使って、回折反射がでるようなことと同じようにやると、実は、このパターンがつくり出す回折点というのは、このようになっているわけです。
高橋:これ、さっきの写真じゃないんですか、準結晶の。
蔡:それと同じものになるわけです。ですから、準結晶、実は発見される前に、すでにこういう図形があったんですね。準結晶の発見とほとんど同じ時期に、同じアメリカの物理学者が、いち早くその構造の面白いところに気付いたわけです。それで、その構造とこのパターンをリンクさせて、このパターンで構造を取りあえず本質的に説明したんです。これは、まさしくつくった回折点は、等間隔ではない。しかも、いろんな五角形が同じようにある。ですから、基本的に準結晶の構造っていうのは、ペンローズパターン、ペンローズタイルで説明されてるわけです。
高橋:ペンローズタイルだったら、こういう回折像ができますっていうシミュレーションみたいな写真なんですか。
蔡:そうですね。同じ回折パターンで示してるけども、実際にシミュレーションで計算すると、同じパターンが出るんです。それは、論文にもそう出てました。ですから、たぶんこういうような論理的に説明したものがあったから、ちょっと待てよと。これは、必ずしも間違いではないというか、面白いところがあると、いろんな研究者が言い始めたんです。 例えば、このパターンを使っていろいろ計算がいろいろできるわけです。ですから、最初、準結晶が発見されて、かなり多くの理論研究者が、飛び付いていろいろやってたわけです。
高橋:でも、すでに数学者がこういうパターンを発見していたっていうのは、不思議ですよね。
蔡:不思議なんですよ。そこは、あたかもシェヒトマン先生の発明というか、発見のおぜん立てというか、布石をしたようなもんだというふうに、今にして不思議でしょうがないですね。
高橋:ペンローズさんは数学者だから、自然界にそういうものがあるかどうかっていうことは、全く関心の外ですよね。
蔡:全く関心がないですね。
高橋:ちょっと面白いですよね。数学パズルみたいな感じで、たった2つの四角形で、ちょっとこういうふうに平面を埋め尽くすことができるっていうのを考えだしたわけですよね。
蔡:そうですね。余談ですけども、ペンローズ自身の専門は、素粒子なんです。
高橋:そうでしたっけ。
蔡:数学者でもあるけど、数学っていうのは自分の趣味でいろいろやってるわけ。
高橋:だから、パズルみたいなお仕事が多いんですね。
蔡:そうなんです。ですから、非常に多才な方です。
高橋:そうすると、理論的にこういうのがあっても不思議じゃないよっていう研究が、たくさん出てきたと。でも、一方で最初のシェヒトマンさんがつくった結晶っていうのは、不安定だからそういう心配はあったんですね。
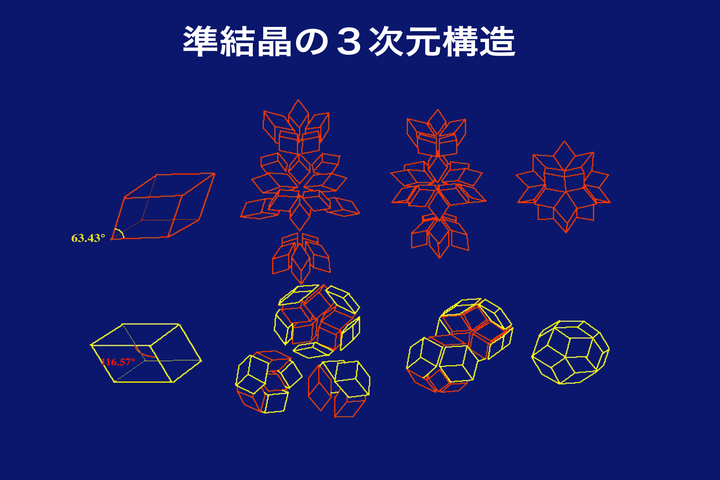
蔡:そうですね。これは、あくまでも2次元なんです。実は、準結晶は、3次元的なものでして、このペンローズパターンをさらに3次元に活用していくのは、この図です。ここを使ってるのは、ひし形の代わりに2種類のひし形六面体を使うわけです。
高橋:立体になったわけですね、さっきの形が。
蔡:それは、ここにありますように、この2つの物を使って。この中のひし形は、黄金比型です。それは、対角線の比がタウになっています。
高橋:これは、ずいぶんぺしゃんこな立体ですね。
蔡:この2通りで、この2つの単位を使って、10個ずつつくると下のほうのような図形ができるわけです。
高橋:このひし形自体は、同じ大きさだからこういう感じで。
蔡:全部それで貼っていけば。
高橋:増やしていけるわけですね。ここの面と面を合わせて。
蔡:そうです。
高橋:そうするとこれが、何角形なんですか。
蔡:これは、ひし形30面体なんです。
高橋:30面体。
蔡:だから、ひし形が30個あります。
高橋:ここが、30個あるわけですね。
蔡:これをこのように2種類の六面体を使って、無限に空間を周期性なく、埋め尽くすことができるわけです。ですから、シェヒトマン先生が見つけた準結晶の構造は、3次元的なものですよね。これが、ある意味では構造に対応するようなものです。非常に難しい、分かりにくいんですけども。
高橋:複雑ですよね。距離が短かったり、長かったりして、規則的じゃないっていうのが分かるのと、あと、これがたくさん並んでるっていうわけじゃないんですよね。
蔡:これが、ある距離を持って並んでるんです。
高橋:その間をまたこれがいろんな形でこれが入ってきたり、これが入ってきたりして。
蔡:そうです。
高橋:これが順番に並んでるわけではない形で、規則的だけど、周期はないっていう3次元。
蔡:フラクタル的な配置になってるんです。
高橋:フラクタル。また新しい言葉が出てきました。
蔡:ちょっとこれ、今はつながないけれども、これをまた30個で、また同じ物をつくってしまうと。自己相似性みたいなもの。
高橋:そうですね。大きい形が分割していくと、また同じような形が出てくると。それがフラクタルですね。
蔡:だから、さっきの黄金長方形をずっと切っていくと同じような。
高橋:あれもフラクタルですね。最初、大きいのも黄金比の長方形だし、小さく切ってもここも黄金比だし、さらに小さく切っても、ここも黄金比だしと。どんどん小さく切っても同じ性質が表れるっていうのが、フラクタルですね。立体になっても、そのフラクタルの性質が。
蔡:3次元の構造も、そういうのを持ってるわけです。
高橋:でも、2次元のペンローズタイルがあるからといって、3次元のこの形がすぐ思い付くってわけでもないですよね。
蔡:そうですね。これを考えた人は、非常にまた優秀な天才数学者ですけど、あんまり論文を発表したことがないです。
高橋:そうなんですか。
蔡:アンマンっていう方が、考えたものなんです。
高橋:それは、シェヒトマンさんの発見より後なんですか。
蔡:発見の前です。
高橋:前に、これが、もうできてたんですか。
蔡:はい。非常に天才的な方なんですけども。実は、4~5年前ですか。初めて準結晶の構造を本当に解明したとき、その中は、これとこの3つの単位からつくられていました。
高橋:初めて構造を解明したって、そんなに時間がかかったんですか。
蔡:ええ。これを見ていただくと分かりますよね。エックス線からどういう原子があるのか分かるのは、やっぱりいろんな数学とか、あるいは物理とか、いろいろ使わないといけない。あと、いい試料がないと、またデータがとれないですね。
高橋:いい試料っていうのは、結晶が安定で、大きなものができていないとってことですね。
蔡:そうです。
高橋:そういうのをつくるところで、蔡先生は、いろいろ手腕を発揮されたわけですよね。
蔡:ちょっとそれ、少し関わりましたけども。それは、5~6年前、初めて構造を解明したっていうのは、結局、ここでは、全部1個1個の原子に対応したわけではなくて、こういう形があって、中に原子がどう分布しているのか、むしろこれは構造解析がやっていることですよね。
高橋:これは、原子モデルではないんですね。
蔡:原子モデルではない。これは、あくまでも図形です。パターンですから。このパターンの中に、どこにどういう原子を置くのか。それは、結晶の構造解析で決めるわけです。図形だけでも終わってしまうんです。だけど、どうして原子が、こういうふうに形をつくるのか。まず、その構造を理解しないといけない。どこにどういう原子があるのか。それが分からないといけない。そのためにやはりいろいろ調べているわけです。
高橋:こういう形を持ったものであると分かってみれば、こういうものも結晶というか、新たな規則性を持った固体であると考えていいって。今までこういうものは、結晶じゃないと考えていたことのほうが、おかしかったなっていうふうに思いますね。
蔡:そうですね。ここまでにはちょっと時間がかかりましたね。1つは、試料があるかないかです。
高橋:試料っていうのは、実物ですね。
蔡:実物の大きな、非常に品質のいい試料です。
高橋:それが、何でなかなかできなかったんですか。
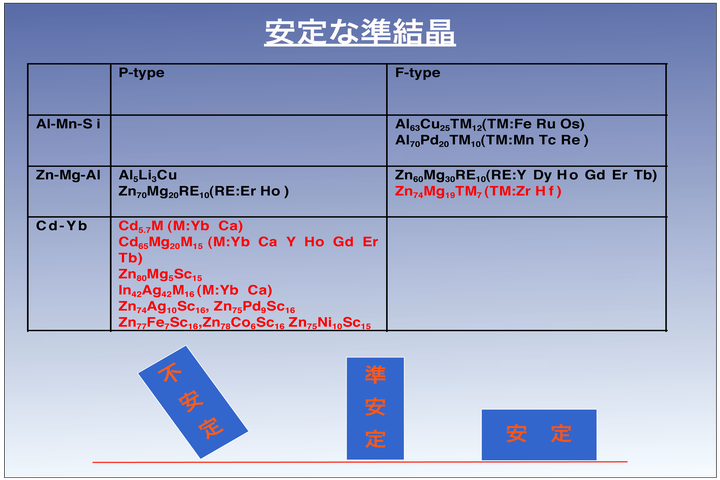
蔡:それは、なかなかできなかったっていうよりも、まず次の図面を見ていただきますと、実は、今まで発見された準結晶は、ほとんど金属からできるんです。シェヒトマン先生が最初やったのは、アルミニウムとマンガンっていう組み合わせなんです。最初は、私がさっき申し上げたように、金属液体から素早く冷やして作ったものなんです。当然みんな、それと同じようにまねして、同じことをやるわけです。で、たぶん、同じような試料をつくるんです。私も、最初はそれと同じようなことをやったんですけども、いろんないたずらも含めて、結局、別にそういうふうに素早く冷やさなくても、普通にもできるっていうことが、幾つか見つけたわけなんです。1つの例として、非常に美しい五角形12面体の形をしているものが、こういうような金属の組み合わせでできました。これは、金属液体の中からゆっくり冷やして、そこの中で徐々に結晶が育っていくわけです。

ですから、素早くじゃなくて、ゆっくり冷却すると、それぞれの原子は、自分が好きな位置に行って、それは安定なものをつくれるわけです。その結果として、こういうような大きな準結晶の単結晶ができるわけです。端から端まで、だいたい2ミクロンぐらいなんですけど。ほかにも、例えば、結晶の単結晶を作っている手法で、シリコンウエハーのような半導体とか、それと同じ手法を用いても、このような大きな準結晶がつくれるようになったんです。ここからだいたい10センチぐらいですけど。径は、1センチぐらいです。こういうのも作れるようになったんです。
高橋:どういう材料を使うかとか、それから3種類の元素を使うんであれば、混ぜる割合は、1:1:1でいいのかとか、その辺はどうやって考えて決めてくんですか。
蔡:それもやっぱり最初の試料をどうやって引っ掛けるのかっていう。それも話せば長いんですけども。例えば、1つどこかに準結晶があれば、すぐに顕微鏡を使って、あるいは分析機を使って、その組成がどうなってるのか、まず調べるんです。ちっちゃくてもいいから、そこから組成を分析すると、これと同じのを作れば、大きなものができるという、最初はそこからです。それは、1個目があれば、これ以外にほかにないのかっていうことをやっぱり考えないといけないです。周期律表を眺めながら。
高橋:似たような性質のものを使っていく。
蔡:そうです、似たような性質の元素でやってみる。あともう1つ重要なのは、いわゆるシェヒトマンが、準結晶を発見するまでに準結晶という概念がないですよね。実は、いろんな状態図というのがあります。状態図というのは、温度と組成で、金属でどこでどういうものができるっていうような図です。これは古くから調べられていて、当時は、準結晶という概念がなくて、いろんな未知相があるわけです。それを準結晶が発見されてから、いろいろ調べると、これは、ちょっとクエスチョンマークっていうか、分からないようなものであれば、それを取りだして調べれば、結果的に準結晶だったのが幾つかありました。
高橋:なるほど、なるほど。
蔡:そういう概念があれば、その概念をもって、昔のいろいろなもの見れば、いろんな新しく見えるものがあるわけです。ここでは別に、最新の装置を使わなくても、ただ新しい概念を持って、新しい視点を持って、古いものを見れば、またいろんな新しいもんが見いだせるってことは、自分の一つの経験なんです。
高橋:そうやって新しい準結晶を、蔡先生は、何種類ぐらい見つけられたんですか。
蔡:ここにあるのは、全部ではないですけれども、私、あるいは私と共同研究者が見つけたものなんです。さっき言ったように、最初をどうやって引っ掛ければいいのか、1つが分かれば、やっぱりなぜできるのかって、まず考えるわけです。そうすると、その共通性を探して、共通性が何かあるのか整理すると、例えば、これとこれが、1原子あたりの電子数とかっていうものが共通するとわかる。ちょっとそこまでは難しくなるんで。
高橋:でも、似ているわけですね、性質が。
蔡:そうです。一番分かりやすいものは、例えば、ここにある鉄、ルテニウム、オスミウムというのは、周期律表で同じ列なんです。だから、最初、アルミ、銅、鉄をやって、次にどれができるのかっていうと、同じ列の元素と置き換えればいい。こういうふうに、1つをひっかければ、同じように規則を出して、またその規則を使って、原理原則を使って、また調べていけば、またいろんなものが見つかると思います。
高橋:でも、その中でも一番安定なものとか、一番性質のいいものとかいうのは、出てくるわけですよね。
蔡:そうですね。一番性質がいいっていうか、例えば、この2つの元素からできているアルミ合金で、構造を初めて解いたわけです。そこが重要なのは、2つの元素からできているということが単純なわけです。それが、非常に重要なんです。今までなかなか構造が解けなかったっていうのは、元素が3つ並ぶと、複雑になってなかなか決めるのが難しかったからです。
高橋:そうやって準結晶、間違いなくあると。いろんな実際の物質も分かってきたと。じゃあ、これは、どういう性質、われわれが使いやすいものなのかっていうところが、次に気になりますよね。
蔡:そもそもシェヒトマン先生が準結晶を見つけたのは、別に準結晶を見つけたくてやったわけではなくて。
高橋:偶然ですね。
蔡:セレンディピティっていうのは、そういうことなんですけれども。彼は、もともとアメリカでサバティカル(研究のための長期休暇)の機会を得て、NBSっていまのNIST(国立標準技術研究所)ですか。そこで仕事をしていたんです。
高橋:もともとイスラエルの研究所にいらして、たまたまその時は、アメリカにいらしてたと。
蔡:そうです。留学っていうか。そこで彼の研究テーマは、金属の急冷組織の電子顕微鏡観察なんです。
高橋:なるほど。
蔡:そのもとは、たぶん強い材料をつくるっていう、最初意識があって、それを調べていくわけです。だけど、彼の作った試料っていうのは、非常にぱりぱりにもろくて、なかなか構造材料というか、良い材料にはなれないんですよ。だから、普通の研究者はあんまり調べなかった。あんまりそれに関心が無いんです。
高橋:役に立たないだろうと思いますね。

蔡:彼が、根気よくちゃんと調べていて、今回のノーベル賞につながったわけです。ですから、もともと構造材料なんですけども、とはいっても、きちんと調べると、いろんな面白いことがあるかもしれないという、彼の一つの例なんです。このスライドに出ているのが、一般的な性質です。やはり、周期がないので、それが理由なのか、電気伝導、あるいは熱伝導がよくないです。電気が流れにくい。
高橋:同じように熱も伝わりにくい。
蔡:というような性質があります。それは、最初、皆、もしかして半導体的な性質があるのかなと思って、いろいろやってたんですけども、結局、やっぱり金属みたいです。もう1つは、やはり硬くてもろいです。だから、構造材料として使うのは難しい。試料をちょっとたたくと、もう粉々になるんです。もろいんです。
高橋:もろいんですね。
蔡:硬いのともろいのは、だいたい同じような現象なんですけども、それに後からヨーロッパがいろいろ調べて、準結晶は、非常に摩擦係数が小さいです。
高橋:すべすべなんですね。
蔡:そうですね。テフロンと同じようなものです。それと、たぶん、これ、連動してるのかもしれないんですけども、撥水性もいい。実は、ほかの同じ系の中で、結晶に比べて比較的酸化されにくいんです。ですから、これをどこで使うのかっていうと、ちょっとぴんと来ないとこがあるんですよね。それもなぜ準結晶が、ノーベル賞を取るまで30年もかかったのかっていう理由の1つなんです。準結晶が発見されたのは84年です。その後の85年と86年、フラーレンと高温超伝導にノーベル賞が出た。やっぱり物性的な華やかさがあるから、いかにもすぐ応用できるっていうふうなイメージであって。準結晶は、そういうような華やかさがないから、結局、基礎でずっと研究してきたっていう感じです。とは言っても、いろんなとこで応用を考えてる方がいまして、その中の1つは。

高橋:シェーバー。
蔡:シェーバーっていうか、ひげそりですね。
高橋:刃にいいんですか、これは。
蔡:実をいうと、準結晶そのものを使うのではなくて、刃の上に準結晶をコーティングするんです。もろいですから、そのまま使えないわけ。
高橋:刃には使えないけれども。
蔡:両面にコーティングするんです。
高橋:すると水をはじくとか、そういうところがいいわけですね。スムーズだとか。
蔡:そうですね。撥水性じゃなくて、テフロンみたいに摩擦係数が小さいから、そうすると、たぶん。
高橋:感触がいいんですね、使うとき。なるほど、なるほど。で、フライパンは、今のテフロンですか。
蔡:そうです。テフロンみたいなんで。これ、ヨーロッパで開発されて、実際、売られていたんです。そこそこは良かったらしいんですけど、ただ傷つくと、まだちょっと。
高橋:もろいところがありますからね。
蔡:やっぱりこれもコーティングでやってるんですよね。それもいろいろ実はやって、そんなにこれっていうようなのはあんまりないです。ただ、これからいろいろ期待される可能性の中では、例えば、準結晶はもろい故に、なかなか主役になれないですよね。コーティングしたりとか。例えば、マグネシウムっていうような柔らかくて、軽い材料の中に、準結晶を分散させて、それを強化させるっていうようなこともやられてる。これは、もしかして、かなり現実味があるかもしれません。もう1つは、熱が伝わりにくいので、熱遮蔽材でも。
高橋:これは、使えそうな感じがしますね。
蔡:これも、たぶん表面をコーティングして使うんだろうと思うんです。3番目は、触媒材料も。もろいですから、粉々にするっていうか、大きな表面積をつくるのは、逆にいいっていう面で、そこの辺で使うと触媒にも一つの可能性があるんです。あともう1つ、最近いろんなところもやってますけど、熱電材料です。熱から電気に伝わる、変えるような素子っていうか、その材料を研究されているわけです。これは、いろんなところで試みられてるんですけど、ただ、どれもすぐマーケットに出てくるものではないんです。
高橋:でも、可能性はいろいろあるということですね。
蔡:準結晶研究も同じなんですけども、25年前、私が研究を手掛けたときには、もうやることないですよって言われまして、言われて25年でやっぱりいまだにやっている。ただやっている研究者の数が少ないですよね。例えば、こういうような応用面を考える研究会があれば、もう少しいろんな可能性が、生まれてくるかもしれません。
高橋:なるほど。分かりました。まだまだお話を伺いますが、いったんここでコマーシャルを入れます。コマーシャルです。
~CM~
高橋:「科学朝日」ゲストはこの方、東北大学多元物質科学研究所教授の蔡安邦さんです。今まで準結晶について、いろいろ伺ってきましたが、蔡先生ご自身が、この準結晶の研究を始められたきっかけっていうのは、何かあったんでしょうか。
蔡:私、実は、博士学位の研究テーマが準結晶でした。ですから、準結晶の実験を始めたのは、1986年の暮れでして、当時、世の中は、高温超伝導ブームでわいていて、うちの研究室もそっちに行ってる人が結構多かったんです。当時っていうのは、シェヒトマン先生の論文が発表されてから、ちょうど2年しかたってないですね。こんなに新しい物だったら、まだいろんなやることがあるんじゃないかと思って、それでテーマを決める時に先生に準結晶をやりたいと、私、申し出たんです。そこに先生も、あと周りのほかの先生たちも、あんなもろい試料だとあんまりやることないですよっていうんでね。ただ、うちの先生が非常に良かったのは、自分がやりたいって言ってきたら、それは、やっぱりやらせてあげようというようなことで、その準結晶を僕は学位論文のテーマとしてやってきたわけです。そういう意味では、先生に感謝しないといけないですね。
高橋:やっていいよって言ってくれた先生に。
蔡:やっぱりそこが、今までの一連の始まりなんです。
高橋:2年後ぐらいだと、まあ正しそうだっていう雰囲気にはなってたんですか。そのシェヒトマンの発見が。
蔡:その時点では、たぶんそれどころではないですよね。毎日、新聞で超伝導、今日は臨界温度が何度になったとか、ああいうニュースばっかりなんですよ。ですから、実は、準結晶が発見されて、さっき話したようにフラーレンやら、超伝導やらが発見された後に、どんどんみんな、物質に対する関心もそういう方向に移っていったんですよね。だから、準結晶をやってるところは、理論の人が多かったんですよね。あと、僕らが所属する研究所は、電子顕微鏡を使って構造を突き止める研究をしている先生もいました。日本は、比較的に研究者が多かったですね。ただ、何をやればいいのかっていうことが、まず問題なんです。やっぱり最初から新しいものを見つけないといけないという、たぶん、そういう課題になったわけです。
高橋:じゃあ、もうドクターコースの時から、準結晶の新しい物質で大きい安定な結晶を見つけてやろうという。
蔡:最初は、もちろんそのつもりはなかったんです。
高橋:ないんですか。
蔡:なんかやらないといけないですけれども、ただ、やっぱりテーマとしてやっていくためには、今までの試料だとちょっと研究ができないんです。それで、やっぱり試料を見せないといけないんです。研究をやるためには、まずそれを作らなければっていうことで始めたわけですね。
高橋:もちろん、それもいろいろな論文読んで、それを参考にして、もしかしてこれなのかなっていうような。

蔡:さっき言ったように、一つがあれば、ほかのいろいろ可能性が出てくるわけですよね。今の準結晶が新しい物質として確立されたっていうのは、やっぱり、ここに示すわれらが見つけた準結晶のクオリティーというか、質です。質がいいということです。これは、エックス線の回折写真なんです。無数の回折点が現れています。しかも、非常に対称性が高い。決して乱れてはいないんです。こういう写真を撮るためには、最低でも試料は、0.2ミリぐらいないと。シェヒトマン先生が見つけたのは、たぶん、0.2ミクロンです。だから、1000倍くらい大きくないとこういう写真はとれない。でも、これがとれないと、準結晶、信用してもらえん。皮肉なことなんですけど。準結晶の発見っていうのは、電子顕微鏡によってなされたんですが、エックス線と電子線の両方の共演が必要だったんですね。で、電子顕微鏡で見た原子像というのは、このようになってるわけです。
高橋:これは、原子の位置をそのまんま表してるんですね。こっちの回折像は、逆空間だけど、こちらは実空間。
蔡:そう、われわれ人間が生きてる空間です。
高橋:確かに原子が、五角形に並んでいると。
蔡:これをいろんな五角形がひけるということは、非常にきれいに欠陥がないということを意味しているんです。また、この原子面の線を引いていきますと、等間隔ではないんです。周期性のないようなもの。ですから、これは非常にいい準結晶なんです。こういうような準結晶が幾つもありますと、これは本当の新しい物質だなって認めてもらえる。
高橋:言ってみれば、シェヒトマン先生は見つけただけで、その後の準結晶の研究をこつこつとずっと進められてきたのは蔡先生というか、蔡先生をはじめとする何人かの研究者たちだった。今回、ノーベル賞はシェヒトマン先生お一人の単独授賞になるのですが、普通だったら、ノーベル賞って3人までもらえます。蔡先生がもらってもよかったんじゃないかっていう声は、特に日本の研究者からは聞きましたけれど。
蔡:それは、確かにそうですね。私がもらうかどうかは別として、結晶学を覆すようなことなので、やっぱり賞をもらわないといけないと僕は思っていました。ただ、やはりわれわれも、このシェヒトマン先生の論文を見てからやったわけです。彼は、準結晶っていうドアをあけてくれた人です。僕以外にいろんな候補になり得る人も結構いましたけども、たぶん、ノーベル委員会は、最初に見つけた1人がもらうべきだと判断したのでしょうね。ただ、自分自身が研究をやっていて、ここまで、ノーベル賞受賞まで関われたことは、これ以上の幸せはないです。受賞理由のような書類の中に、ちゃんと論文が引用されているから、私にとってはそれで十分満足です。
高橋:もし、先生がノーベル賞を受けられていたら、日本に住んでいる外国生まれの研究者として初めてっていうことになったんですよね。「たら」とか、「れば」とか言ってもしょうがないことではありますけれども、外国で生まれて、研究生活をずっと日本で送ってらっしゃる。日本における外国人研究者、もう外国人と言ってはいけないのかもしれないんですけれども、という立場から見て、今、日本の研究環境というのはいかがですか。
蔡:もし、さっき言ったような賞が授賞されれば、それは私だけじゃない、現時点で日本で研究している外国人にとって一つの励みになるんですけども。今は外国人研究者もかなり増えています。あと、研究環境でいうと、自分の経験から言いますと、比較的運が良くて、いた所、いた所で人に恵まれて、いろんな素晴らしい研究仲間と一緒にやれたんです。また特に、研究予算にあまり不自由した記憶もなくて、そういう意味では、準結晶というのはあしたにでもすぐ使える材料でもないんですけども、それでもちゃんとじっくりやらせていただけた。そういう意味では、今の世の中、そんなにないんじゃないですか。私的には、研究環境は文句ないです。
高橋:なるほど。日本は、これからもやっぱり科学研究でいろいろ実績を残していかなければならないと思いますけども、そこで外国人研究者の活躍もどんどん増えていくのが望ましいことだと思いますので、今日は、本当に貴重なお話、いろいろありがとうございました。
蔡:どうもありがとうございました。
高橋:「科学朝日」この辺で失礼いたします。
有料会員の方はログインページに進み、デジタル版のIDとパスワードでログインしてください
一部の記事は有料会員以外の方もログインせずに全文を閲覧できます。
ご利用方法はアーカイブトップでご確認ください
朝日新聞社の言論サイトRe:Ron(リロン)もご覧ください