カナダ製の世界初マシンは、日本の「量子アニーリング」理論を応用
2017年12月22日
量子コンピューターをめぐって、業界がざわついている。内閣府や科学技術振興機構が「世界最大規模の量子コンピューター」とうたう成果を発表し、異論が吹き出しているからだ。開発にかかわった身内からも「量子コンピューターではないのでは?」と疑問が出ている。
 カナダの企業が開発した世界初の量子コンピューター「Dウェーブ」
カナダの企業が開発した世界初の量子コンピューター「Dウェーブ」これからますます、いろんな話題が登場しそうな量子コンピューター。そこで今回、カナダで開発された初の量子コンピューター「Dウェーブ」の原理を見ていこう。旬の話題に乗っかるための第一歩だ。
「巡回セールスマン問題」と呼ばれる難問がある。いくつもある街をすべて効率よく訪問してから戻りたいセールスマンが、それぞれの街を1回ずつ訪ねる最短経路を求める問題だ。単純そうだが、じつはこの問題にきれいな解法はない。つまり、すべての経路の組み合わせを総当たりで確かめるしか、解く方法はないとされている。
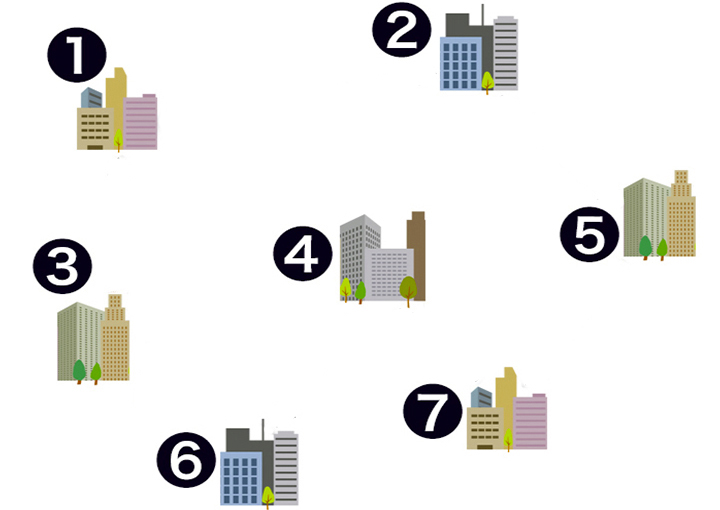 すべての街を最短距離で巡回するには?
すべての街を最短距離で巡回するには?しかし量子コンピューターなら、あっさり解けると期待されている。「総当たり」という作業こそ、量子コンピューターの得意技だからだ。
では、どうやっているか。まずは巡回セールスマン問題を見よう。この問題を解くには、
「1番目は街1か?」「1番目は街2か?」「1番目は街3か?」……
「2番目は街1か?」「2番目は街2か?」「2番目は街3か?」……
「3番目は街1か?」……
という組み合わせのすべてについて、それぞれイエスかノーで場合分けをする。イエスなら「+1」、ノーならば「0」に、それぞれの街同士の距離をかけて合計すれば全体の距離になるから、最短の組み合わせを選べばばよい。
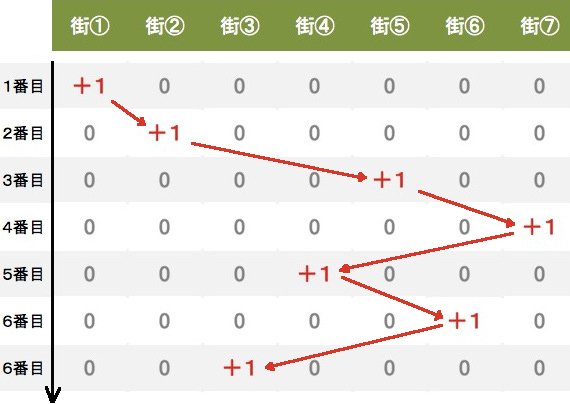 街を訪ねる順番の組み合わせを探す
街を訪ねる順番の組み合わせを探す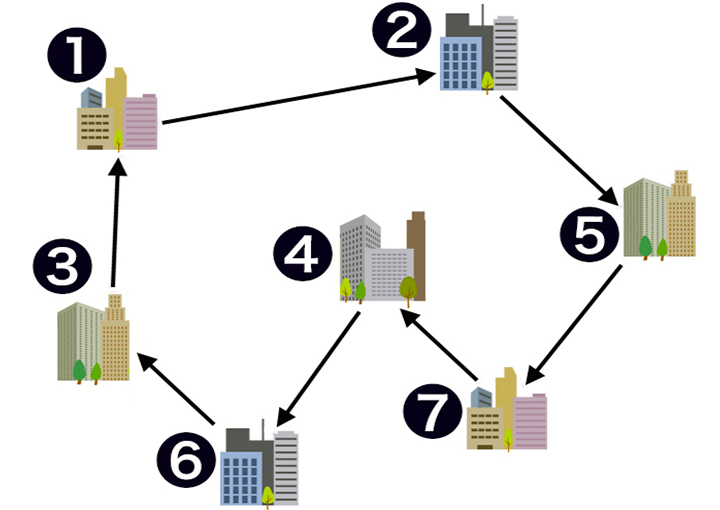 見つかった最短の経路は……
見つかった最短の経路は……では、量子コンピューターの動作原理はどうだろう。利用するのは、原子や電子が持っている「スピン」という特殊な性質だ。
スピンは磁力を生みだす根本となる物理量で、上向きなら「+1」、下向きなら「-1」の値をとる。このスピンを平面に並べたとき、全体のエネルギーはそれぞれのスピン間の相互作用によって決まる。つまり、
「スピン1〜2の相互作用は?」「スピン1〜3の相互作用は?」……
「スピン2〜3の相互作用は?」「スピン2〜4の相互作用は?」……
「スピン3〜4の相互作用は?」……
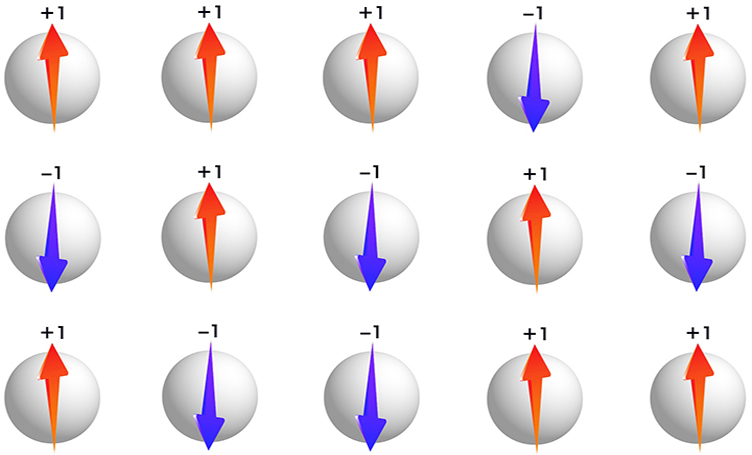 平面上に並んだスピンの相互作用は
平面上に並んだスピンの相互作用はこの「すべての組み合わせの合計」という手順の類似性を応用するのが、いまの量子コンピューターだ。いわば、自分が解きたい問題を量子の関係に当てはめて、エネルギーがどう変化するかをシミュレーションするような仕組みだといえる。
ポイントは、この計算をするときに「量子の重ね合わせ」という奇妙な現象を利用することだ。量子力学が扱うミクロの世界では摩訶不思議なことに、このスピンの値が同時に
有料会員の方はログインページに進み、デジタル版のIDとパスワードでログインしてください
一部の記事は有料会員以外の方もログインせずに全文を閲覧できます。
ご利用方法はアーカイブトップでご確認ください
朝日新聞社の言論サイトRe:Ron(リロン)もご覧ください