検査がもっている不確実性と認知バイアス
2020年03月27日
メディアは新型コロナ一色だ。特に最近はPCR検査をめぐって議論が起きている。WHOは「とにかく検査、検査、検査」とあおり、韓国では日本の18倍もの検査が実施されている(3月19日、FNN.PRIME)。欧米メディアも「韓国を模範」とするか(3月18日、ロイター)、むしろ「検査を限定する日本のやり方に注目」するか(3月25日、時事)、分かれた。
 北九州市小倉南区の職員が新型コロナウイルス感染者と判明し、区役所を消毒する作業員=2020年3月24日、藤脇正真撮影
北九州市小倉南区の職員が新型コロナウイルス感染者と判明し、区役所を消毒する作業員=2020年3月24日、藤脇正真撮影
まずは読者にひとつ問題を出そう。
問題
今ある人がPCR検査で「陽性」と判断されたとする。この人が本当に感染している確率は、どれほどか? ただし、検査の「感度」=70%、「特異度」=98%、真の感染率=1%とする。(検査に至った経緯や、発熱・咳など他の所見は無視する)。
ここで感度とは、本当に感染している人を正しく「陽性」とする確率のことだ。また特異度とは、感染していない人を正しく「陰性」とする確率をいう。「感度が70%というんだから、答えはおよそ70%」と直感的に思った読者が多いのではないか。あるいは、こうあらためて訊かれれば警戒するが、ニュースなどで「クラスターで陽性が10人」=「10人が感染」と素直に受け取ってしまう向きも多いだろう。
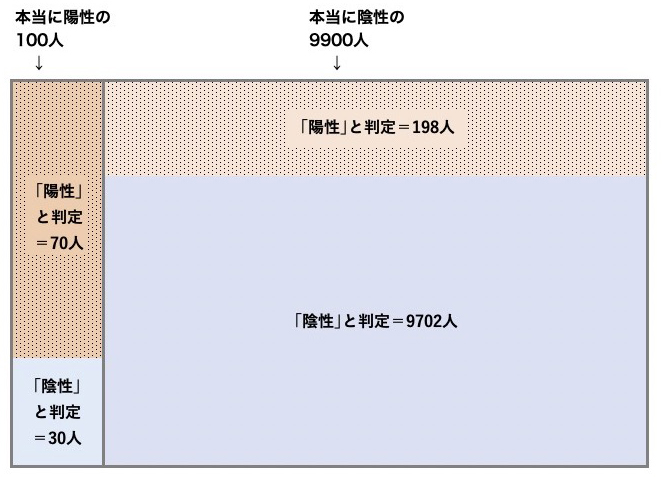 1万人を検査すると、70人+198人が陽性と判定される。本当の陽性は70人だから、結果が正しい確率は70÷268=26%
1万人を検査すると、70人+198人が陽性と判定される。本当の陽性は70人だから、結果が正しい確率は70÷268=26%正解は、約26%だ。判定が「陽性」でも、本当の感染者は10人中3人以下ということだ。これはかなり直感に反するだろう。驚きついでに、もうひとつ質問。この確率(陽性で、本当に感染している確率)は、母集団の感染率(たとえば日本全体で、真に感染している人の割合)の影響を受けるだろうか。「感度が変わらない以上、変わらない」と答えた方、残念ながらまたもや誤答だ。
よく知られる確率のイリュージョン(認知心理学で「ベイズ確率の反直感性」と呼ばれる現象)が、起きている。
なぜ正解がこうなるのか、順を追ってわかりやすく説明しよう。まず検査の「正解」「不正解」には、それぞれ2種類あることを、「信号検出理論」の観点から理解したい。信号検出理論というのは通信の評価から発した理論で、発信した信号にノイズが混じるとき、受信側が正しく信号を検出できるかを問う。転じて、感覚・知覚の研究や神経科学でも、応用されている。
表を見てもらえばわかる通り、まず信号(医療検査なら被験体)の側に、信号(感染)あり/なしの二通りがある(表の左欄)。これに対し応答(検査結果)は、いうまでもなく陽性/陰性の二通りだ(上段)。
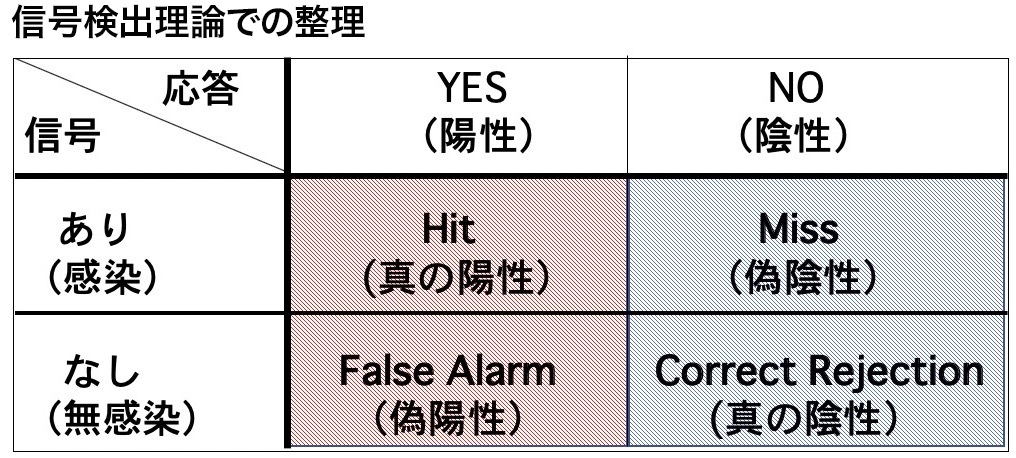 実は「陽性」判定にも「陰性」判定にも2種類がある。PCR検査は感度が低いため、特にこの偽陽性が増える問題がある
実は「陽性」判定にも「陰性」判定にも2種類がある。PCR検査は感度が低いため、特にこの偽陽性が増える問題がある
答えが26%と驚くほど低いのは、この二つ目(False Alarm)が実は大きな割合を占めているからだ(図参照)。逆に、「陰性と判定されて、実際には感染している確率」は、この条件下では極めて低く、0.3%しかない。つまり偽陰性はほとんど出ない。
言ってみればこの検査方法は、目の粗い網のようなものだ。本当の魚(感染者)をしばしば逃してしまうが、小魚(非感染者)を誤って捉えることはほとんどない。感染者10人のうち7人にしか正しく「陽性」の判定を出せないほど、網の目は粗いが、本当の被感染者を「陽性」と間違えて網にかける割合は2%しかない。
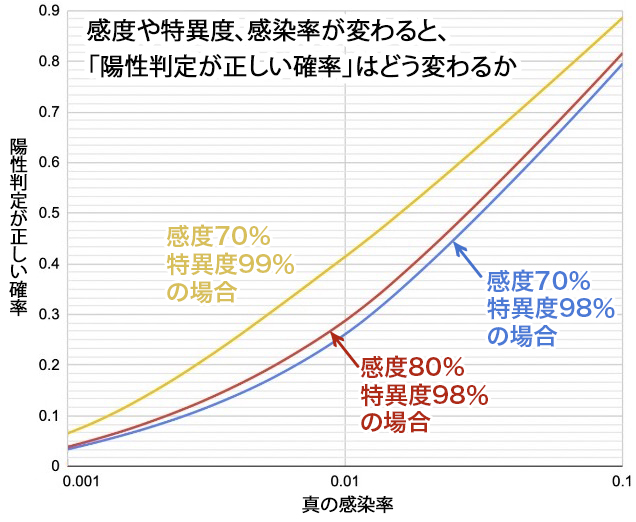 横軸は対数目盛り。左端は1000人にひとり、右端は10人にひとりが本当に感染している場合を示す。(coding by Kensuke Shimojo)
横軸は対数目盛り。左端は1000人にひとり、右端は10人にひとりが本当に感染している場合を示す。(coding by Kensuke Shimojo)
検査についてひとつ強調しておきたいのは、上記確率が母集団の感染率によって大きく変わることだ。感度、特異度の値によっても、いくらか変わってくる(グラフ参照)。
ここまで、検査の不確実性を確率で論じてきたが、現実に何か示唆があるだろうか。
有料会員の方はログインページに進み、デジタル版のIDとパスワードでログインしてください
一部の記事は有料会員以外の方もログインせずに全文を閲覧できます。
ご利用方法はアーカイブトップでご確認ください
朝日新聞社の言論サイトRe:Ron(リロン)もご覧ください