数理科学からみた新型コロナ問題
2020年07月27日
しかし一方、機会あるごとに、感染症対策における感染症数理モデルの実践的意義を主張してきたし、関連する教育や啓発に努めてきた経緯もある。そこでいささか思うところを披瀝させていただくこととした。
今回の事例を語るために、少し過去を語ることをお許し願いたい。さきに私がデータを扱わないと言ったが、それは四半世紀前に東大数理に移籍してからのことであり、それまで勤務していた厚生省人口問題研究所においてはデータ分析も人口推計もおこなってきた。また当時問題となったエイズ流行問題では、厚生省エイズ疫学研究班で感染動向の分析にも関わった。その頃の経験からすると、今回の事態はまさに隔世の感があった。
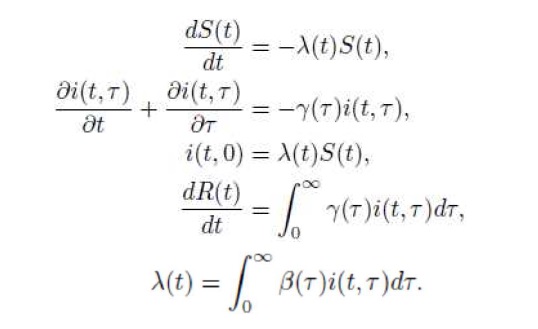 1927年に現れた前期ケルマック・マッケンドリックモデルの式。これは人口再生産のない封鎖系における一回の感染症流行を記述している。S(t)は時刻tにおける感受性人口サイズ、i(t,τ)は感染からの経過時間(感染齢)τにおける感染人口密度、Rは回復人口サイズである。βは感染率、γは回復率であり、λは感染力を示す。βやγが感染齢に依存しない定数であれば、よくしられた常微分方程式系に還元される。
1927年に現れた前期ケルマック・マッケンドリックモデルの式。これは人口再生産のない封鎖系における一回の感染症流行を記述している。S(t)は時刻tにおける感受性人口サイズ、i(t,τ)は感染からの経過時間(感染齢)τにおける感染人口密度、Rは回復人口サイズである。βは感染率、γは回復率であり、λは感染力を示す。βやγが感染齢に依存しない定数であれば、よくしられた常微分方程式系に還元される。感染症数理モデルの近代的基礎は1920年代から30年代にかけて、英国の医師マッケンドリックと物理化学者ケルマックの一連の共同研究(微分方程式モデル)によって築かれた。その発展は70年代までは非常に緩慢であったが、80年代に数理生物学の勃興とともに急速に発展するようになり、おりからのエイズパンデミックによって多くの資金・人材が投入され、統計的な手法の開発とともに、感染規模推計、流行予測、体内のウイルス動態解析などに利用されるようになった。その後、牛海綿状脳症(BSE)や新型インフルエンザ、SARS(重症急性呼吸器症候群)、MERS(中東呼吸器症候群)、エボラ出血熱等の相次ぐ新興・再興感染症の発生への対処を通じて、感染症疫学における有力な手法として定着するに至ったといえる。
しかし、90年代のエイズ危機が叫ばれた頃は、日本には感染症数理モデルを流行分析に活用できる研究グループは存在しなかった。当時の感染者推計等は非常に素朴なもので、まったく世界の水準に達していなかったのであるが、幸いなことにエイズの急激な流行は日本ではおきなかった。これは日本人の性的活動性の低さのゆえであったかもしれないが、そのために、保健医療体制に過大な負荷をかけることもなく、したがって理論疫学的対応の不備が問題化することもなかったのである。
そのような構図は、2000年代以降に相次いだ感染症危機においても繰り返され、日本における感染症数理モデルの研究と政策実装は世界に大きく後れをとった。ちなみに、今回有名になった感染症の基本再生産数という概念は、2009年の豚インフルエンザ危機の時に初めて新聞紙面上に紹介されたが、
有料会員の方はログインページに進み、デジタル版のIDとパスワードでログインしてください
一部の記事は有料会員以外の方もログインせずに全文を閲覧できます。
ご利用方法はアーカイブトップでご確認ください
朝日新聞社の言論サイトRe:Ron(リロン)もご覧ください