4桁の数字であそぶ タクシーのナンバーに特別な意味見つけた天才数学者ラマヌジャン
2022年01月10日
正月三が日、皆さんはどのように過ごされただろうか。私は何をやっていたかというと、4桁の数字と「格闘」していた。
数字と相撲を取っていたわけではない。4桁の数字を使ったある種のパズルの沼に引き込まれ、3日間をほぼそれに費やしてしまったのであった。数字をもてあそんでいたというべきかもしれない。あるいは、数字にもてあそばれたというべきか。

例を示そう。いずれも近所で採集してきたナンバープレートである。
左上の6821は「6=8-2*1」が答えの一つだ。右上の3467も「3-4=6-7」と簡単に解ける。だが左下の1983はやや難しい。しばらく考えて解けたが、やや工夫が必要だ(答えは記事の末尾に書く)。右下の6763はかなり難しく、現時点では答えが浮かばない。
出会った数字を見て、解ければちょっとうれしく、解けなければ少し悔しい程度のたわいもない話だ。だが小みそかの12月30日、こんなことを思いついた。
 =shutterstock.com
=shutterstock.com私自身は年賀状を出さなくなって久しいが、年賀状に「2022」などと大きく西暦を書くのは定番のデザインだから、それが等式になっていれば格好いいだろう。「今後の年賀状のデザインにも使えるように」。そんなことも考えた。
車のナンバープレートなら、解けない数字の車はやり過ごせばいいし、すぐ忘れてしまう。だが西暦は連番なのでそうはいかない。一つずつ順に攻めていくしかない。

するとフェイスブック仲間で、かつての同僚が「科学部だった先輩が、年末にどうでも良いことを思いつき悩まれていました」と紹介してくれ、彼の友人たちから次々と助け舟が出た。
「2029 20=|2-√9|」「できた! 2028 (2+0)*√2=√8」「2025 2!+0!=|2-5|でけた」「2033 20=3/3」と。ツイッターでも2027の“近似解”を提案してくれた人がいた(これも記事末尾に)。
ちなみに「!」は階乗を表す記号である。3!と書くと3の階乗3×2×1=6を表す。また、|2-3|のように2本の「|」で式を挟むと絶対値を表し、この場合2-3=-1で、絶対値は1となる。また掛け算は小学校や中学校では「×」を使うことが多いが、高校では「・」を使うこともある。またエクセルなどコンピューターでは「*」を使うのが一般的だ。
2021で始めた戦いが2032まではつながった。「そうか、意外と続けられるのか」と思い、一歩一歩進むことにした。一日中こればかりやっていたわけではないが、元日深夜には2100を超えて2200に到達。さらに2日に2300、3日夜には2400を達成した(結果は連続ツイートに)。
やってみると楽なところと苦しいところがあった。楽なのは例えばこのあたりだ。
2211 2-2=1-1または2/2=11
2212 2/2+1=2または2/2=12
2213 2*2-1=3または2/2=13
2214 2*2*1=4または2/2=14
2215 2+2+1=5または2/2=15
同じパターンの繰り返しが可能で、自転車をこがずに坂道を下りる感じだ。
一方、難所では自転車には乗れない。ごく簡単に解ける数字と数字の間に、急に高い峰がある。降りて注意深く押して歩く。特に2200年代後半、2300年代は苦しかった。
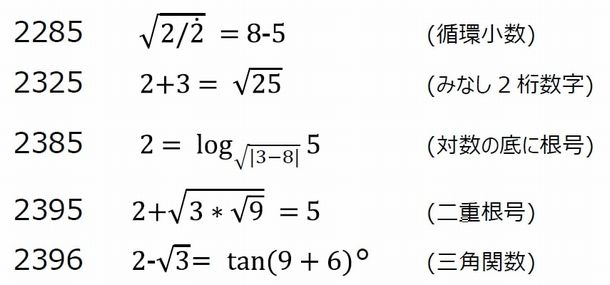
2325では、苦し紛れに2と5を一つの数字「25」と見なすことにして切り抜けた。そうやって手元の武器を増やしていった。
2385は難所中の難所だった。廃線になったが、信越線の碓氷峠越えみたいなものか。半日近く答えが浮かばなかったが、真ん中の百の位の3と十の位8の差が一の位の5になることに気づき、対数関数の底に根号を入れるという荒業で何とか解決した。
2395は根号の中に根号を入れる二重根号でねじ伏せた。
新たな助け舟もあった。2396は、自分では2395と同じパターンで処理したが、学生時代からの友人が三角関数の半角公式を応用するという秀逸な手法を提案してくれた。これはなかなか思いつかない。
やっているうち、「数字のやばさ」のようなものを感じるようになった。5や7が絡むと解くのが難しくなる気がした。一方で2は扱いやすい。数学とはいえないかもしれないが、肌感覚としてそういうものを感じた。
孤独な戦いを続ける中で思い出したのは、高校で習った積分だった。どんな関数でも微分はできるが、積分はそうはいかない。ちょっと複雑な関数になると、「こんなの誰が考えたのか」と思いたくなるテクニックを使ってやっと積分できる。そんな感覚だ。
「いい国(1192)つくろう鎌倉幕府」「人世むなしく(1467)応仁の乱」みたいな日本史の西暦語呂合わせづくりの苦労にも思いをはせた。語呂合わせなら、多少の字余りや字足らず、舌足らずなどの妥協も許容されるだろう。また、秀作を集めて参考書をつくれば売れるかもしれない。
だが私の「西暦で等式」は、一応、数学なので数余りや数足らずは許されない。参考書にも論文にもならないだろう。そんなこんなで三が日がつぶれた。
ここまでなら、単なる正月のたわ言になってしまうが、前述の友人が「車のナンバープレートってラマヌジャンみたいやな」とメールしてきたのである
有料会員の方はログインページに進み、デジタル版のIDとパスワードでログインしてください
一部の記事は有料会員以外の方もログインせずに全文を閲覧できます。
ご利用方法はアーカイブトップでご確認ください
朝日新聞社の言論サイトRe:Ron(リロン)もご覧ください